29. Transpose of a Matrix
Transpose of a Matrix
There were a few Kalman filter equations that required the transpose of a matrix. You can identify these matrices because they have a T superscript. For example the transpose of matrix \mathbf{A} is written \mathbf{A^T}
These were the three equations that contained the transpose of a matrix:
\mathbf{P_{k|k-1}} = \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} + \mathbf{Q_{k}}
\mathbf{S_{k}} = \mathbf{H_{k}} \mathbf{P_{k|k-1}} \mathbf{H_{k}^T} + \mathbf{R_{k}}
\mathbf{K_{k}} = \mathbf{P_{k|k-1}} \mathbf{H_{k}^T} \mathbf{S_{k}}^{-1}
What exactly is the transpose?
You can think of the tranpose as switching rows and columns. The matrix rows become the columns or alternatively you can consider the columns become the rows.
Here is an example. If you start with this matrix,
\begin{bmatrix}3 & 25 & 9 & 2 & 4 \\ 7 & 15 & 6 & 92 & 17 \\31 & 18 & 0 & 11 & 8\end{bmatrix}
the transpose would be
\begin{bmatrix}3 & 7 & 31 \\ 25 & 15 & 18 \\ 9 & 6 & 0 \\ 2 & 92 & 11 \\ 4 & 17 & 8\end{bmatrix}
The original matrix was size 3x5. The transpose is 5x3.
To get a better understanding of what is happening, this image is color coded to match values from the original matrix and the transpose of the matrix. If you think of switching the rows and making them into columns, the matrix operation looks like this:
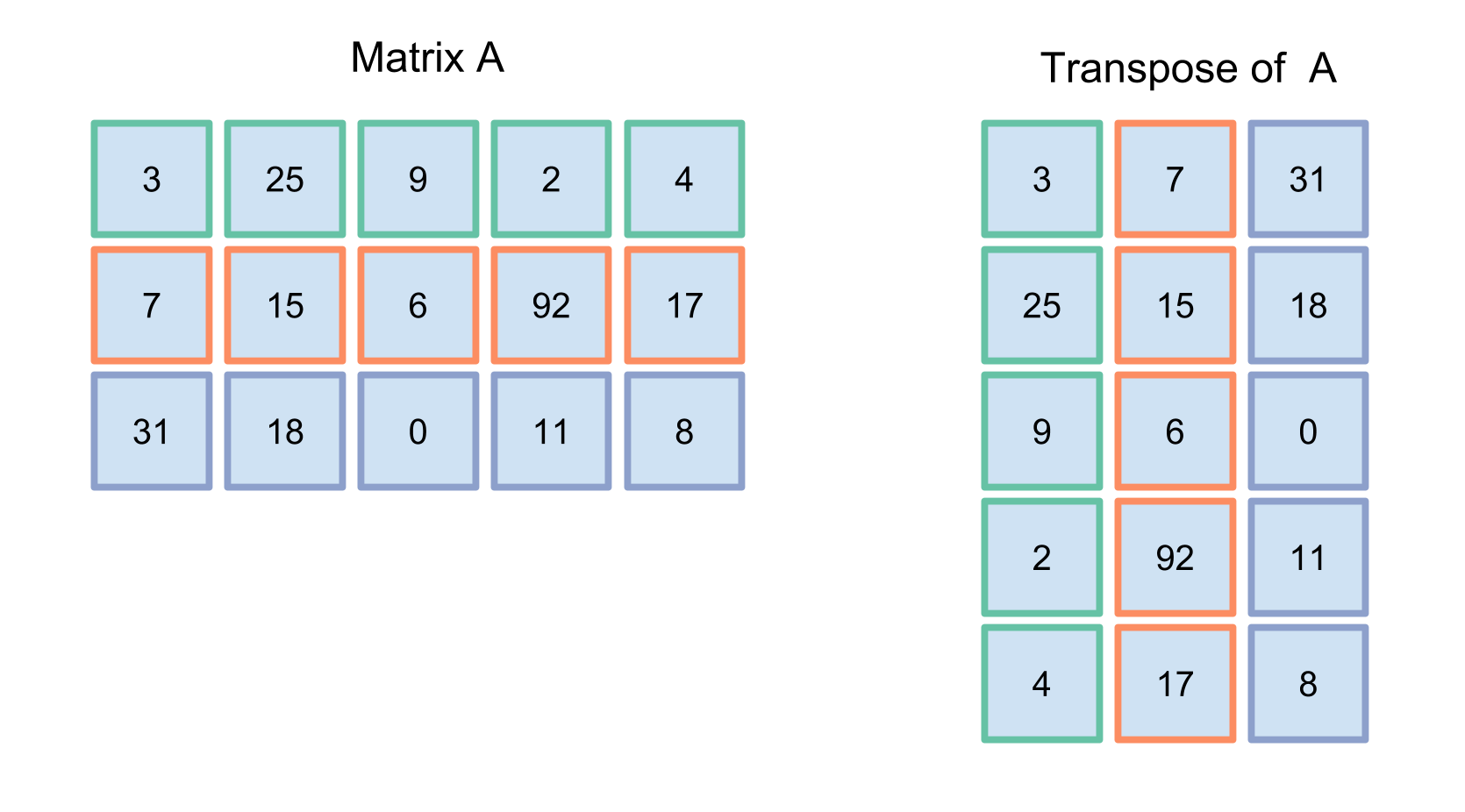
But you could also think of transposing the columns into rows:
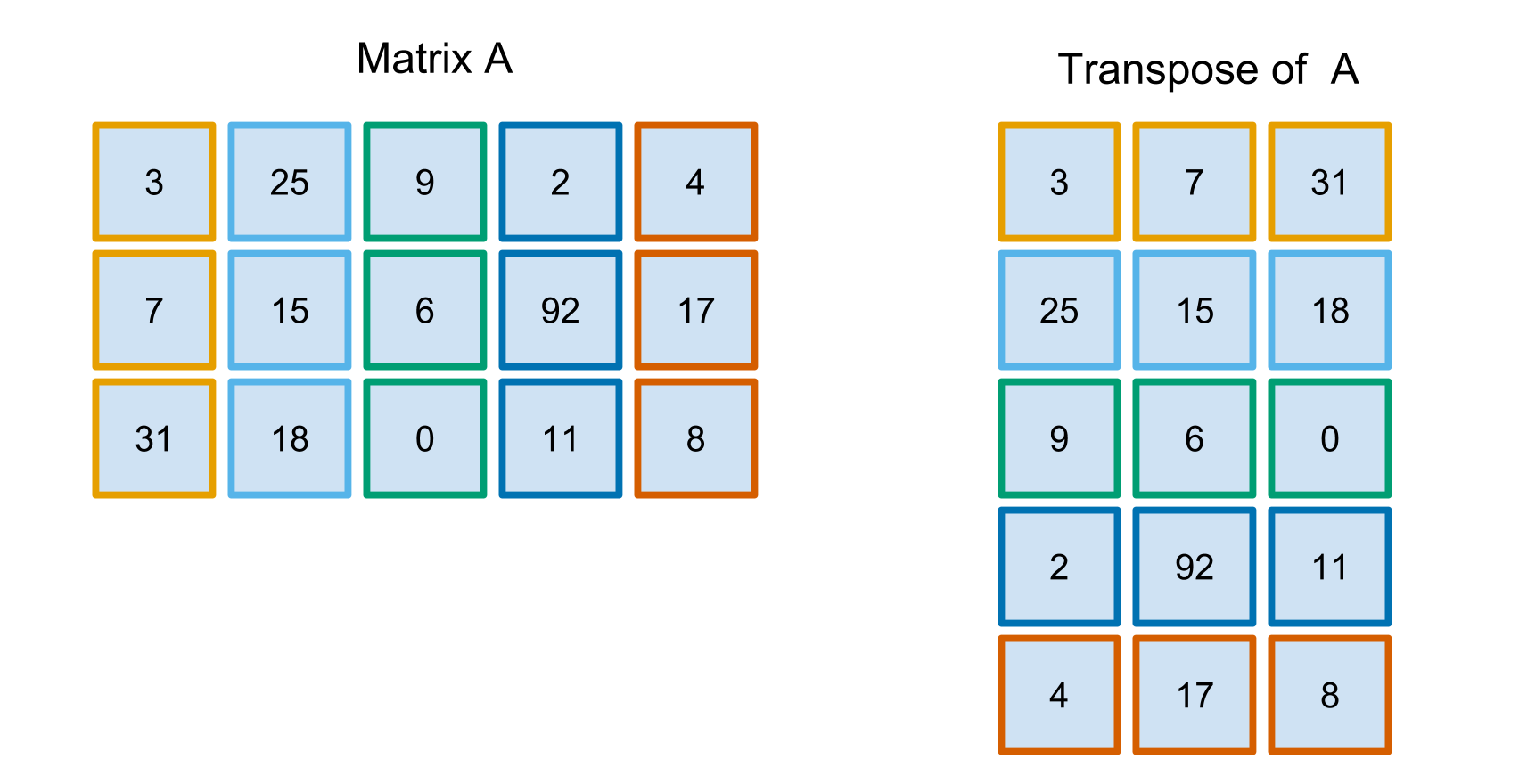
Mathematically, you are switching around the i and j values for every element in the matrix. For example, the element in the 3rd row, 4th column is 11. For the transpose of the matrix, 11 is now in the 4th row, 3rd column. The formal mathematical definition of the transpose of a matrix is
[\mathbf{A^T}]{ij} = [\mathbf{A}]{ji}
Motivation for Calculating the Transpose
In order to use the Kalman filter equations, you need to calculate the transpose of both the \mathbf{F} \text{ and } \mathbf{H} matrices.
But there is also another place where you could use a matrix transposition: when carrying out matrix multiplication. In the previous exercises for matrix multiplication, you wrote a function that returned a column of a matrix. You needed matrix columns in order to find the dot product of a row from matrix \mathbf{A} and a column from matrix \mathbf{B}.
Here is a reminder of what that looked like:
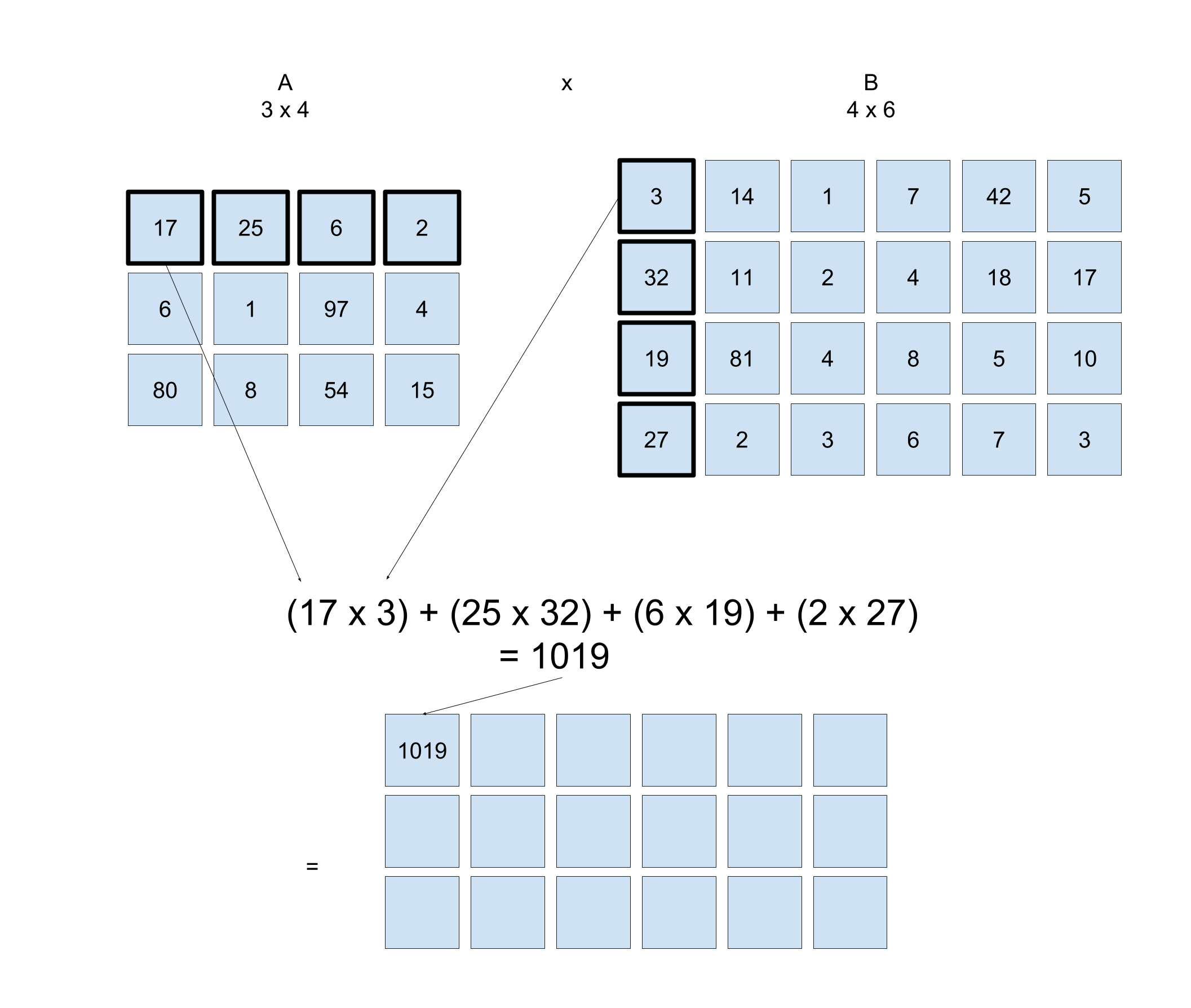
But what happens if you take the transpose of matrix \mathbf{B}? All of the columns in \mathbf{B} become rows. Your matrix multiplication function then involves finding the dot product between rows of \mathbf{A} and rows of \mathbf{B^T}:
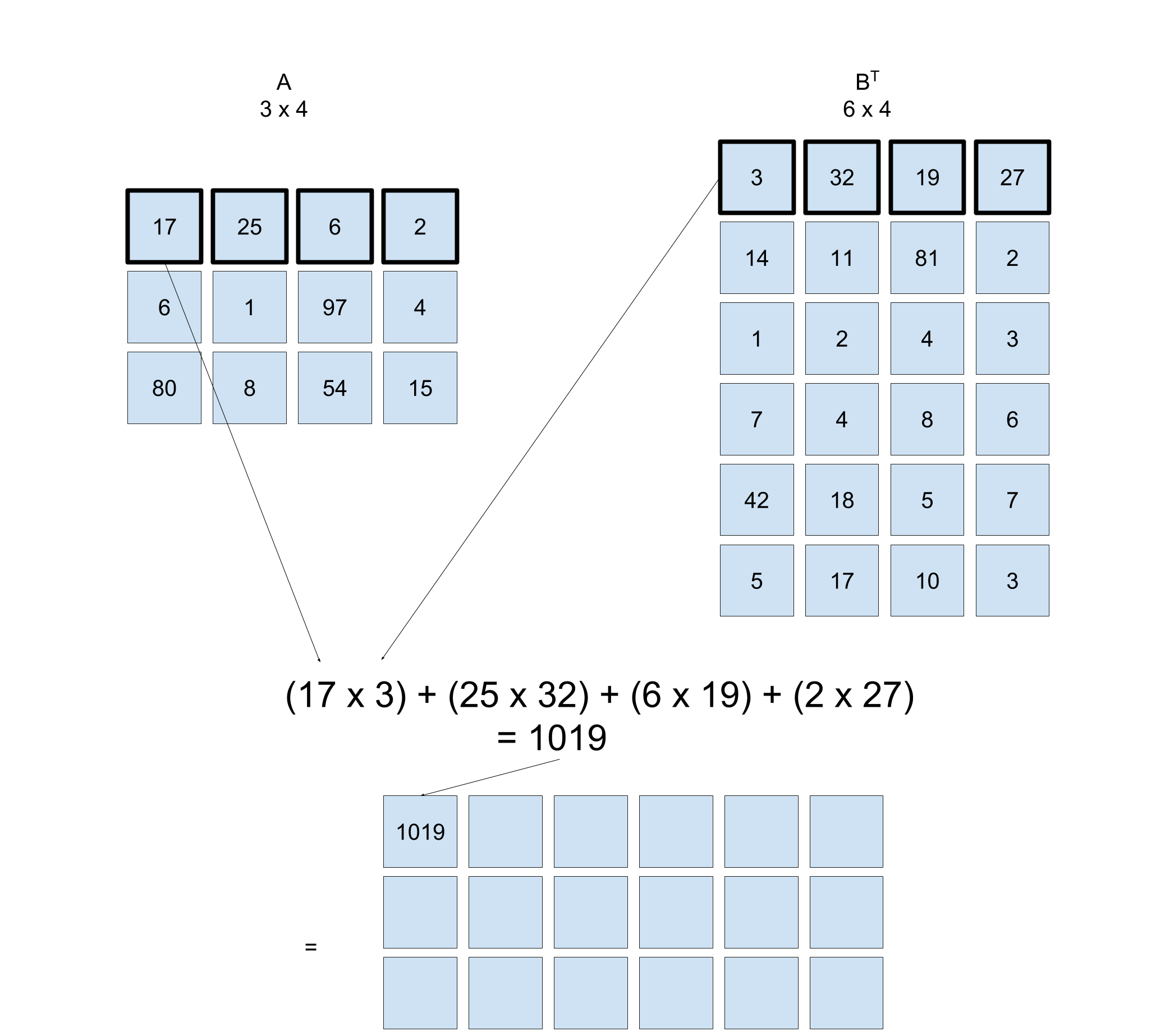
Dot product between rows of A and transpose of matrix B
You are not calculating the product of AB^T. Instead, you are taking advantage of matrix transposition to make matrix multiplication easier to code.
In the previous coding exercises, the get_column function you built to change a matrix column into a horizontal vector was essentially a transpose.
In the coding exercises for this part of the lesson, you will not only write a transpose function but also write a new multiplication function that takes advantage of the matrix transpose.
Coding the Transpose of a Matrix
This is a similar problem to what you have already seen; you'll need to use nested for loops. But what exactly will this nested for loop look like?
You could iterate through the matrix like you've done already with the rows in the outer loop and the columns in the inner loop:
for i in range(len(matrixA)):
for j in range(len(matrixA[0])):
print(matrixA[i][j])The transpose of the matrix would need to store each i, j element inside a new matrix with position j, i. But how are you going to populate this new matrix? You would probably first need to create an n x m list within a list and populate this nested list with empty values. That sounds complicated.
Is there a more efficient way to code matrix transposition? Think about how you could start iterating through the columns in the outside for loop and the rows on the inside for loop.
Go to the next part of the lesson to write your code.